Module « math » Python 3.12.1

Fonction factorial - module math

Signature de la fonction factorial

 def factorial(value: int) -> int

Description

Cette fonction calcule la factorielle d'un entier positif. Cette fonction mathématique est couramment notée n! (ou n représente l'entier positif pour lequel calculer la factorielle). La factorielle d'un entier positif est définie comme le produit des nombres entiers strictement positifs inférieurs ou égaux à n et la factorielle de 0 vaut 1. Voici la définition mathématique :

Définition mathématique de la fonction factorielle.

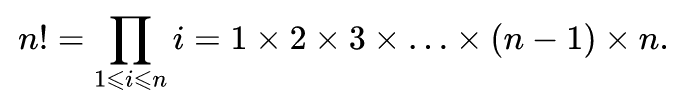
Voici, à titre indicatif, les premières valeurs de la fonction factorielle.

Valeur	Factorielle
0!	1
1!	1
2!	2
3!	6
4!	24
5!	120
6!	720
7!	5 040
8!	40 320
9!	362 880
10!	3 628 800
11!	39 916 800
12!	479 001 600
13!	6 227 020 800
14!	87 178 291 200
15!	1 307 674 368 000

help(math.factorial)

Find n!.

Raise a ValueError if x is negative or non-integral.

Paramètre

Paramètre	Description
value : str	L'entier positif pour lequel calculer la factorielle.

Valeur de retour

La valeur de retour est de type str.

Elle correspond à la factorielle de l'entier positif passé en paramètre

Exceptions

```
 TypeError :
```
Une exception de ce type sera déclenchée si la valeur passée en paramètre n'est pas un entier.
```
 ValueError :
```
Une exception de ce type sera déclenchée si la valeur passée en paramètre est négative.

Exemple(s) de code

La factorielle est notamment utilisée dans les définitions des séries de Taylor. Les fonctions mathématiques usuelles et notamment les fonctions trigonométriques peuvent être définies par une telle série. L'exemple ci-dessous vous montre comment calculer la fonction sinus à partir de la factorielle.

Définition mathématique de la fonction sin par une série.

Exemple d'utilisation de la fonction math.factorial.
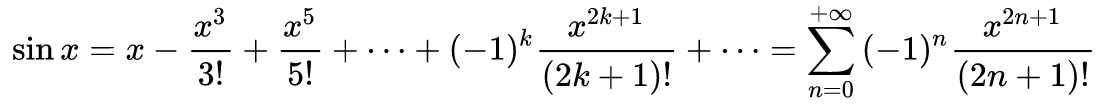
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21	#!/usr/bin/python3 import math def my_sinus(value: float, rank: int) -> float: accumulator: float = 0 while rank >= 0: num = value ** (2 * rank + 1) den = math.factorial(2 * rank + 1) accumulator += ((-1) ** rank) * num / den rank -= 1 return accumulator for r in range(10): print(f"my_sinus(1, {r}) =", my_sinus(1, r)) print("Valeur de référence : math.sin(1) = ", math.sin(1))

#!/usr/bin/python3

import math


def my_sinus(value: float, rank: int) -> float:
    accumulator: float = 0

    while rank >= 0:
        num = value ** (2 * rank + 1)
        den = math.factorial(2 * rank + 1)
        accumulator += ((-1) ** rank) * num / den
        rank -= 1

    return accumulator


for r in range(10):
    print(f"my_sinus(1, {r}) =", my_sinus(1, r))

print("Valeur de référence : math.sin(1) = ", math.sin(1))

Exemple d'utilisation de la fonction math.factorial.

dans l'expression python -1 ** 2, l'opérateur unaire de signe est moins prioritaire que l'opérateur **. En conséquence l'expression précédente est équivalente à -(1 ** 2) et calcule -1. Vous comprenez donc mieux la présence des parenthèses autour de la valeur -1 dans la correction : (-1) ** rank.

c'est la table de précédence des opérateurs du langage qui définit la priorité des différents opérateurs.

Et voici les résultats produits par cet exemple.

$> python3 sample.py
my_sinus(1, 0) = 1.0
my_sinus(1, 1) = 0.8333333333333334
my_sinus(1, 2) = 0.8416666666666667
my_sinus(1, 3) = 0.841468253968254
my_sinus(1, 4) = 0.8414710097001764
my_sinus(1, 5) = 0.841470984648068
my_sinus(1, 6) = 0.8414709848086585
my_sinus(1, 7) = 0.8414709848078937
my_sinus(1, 8) = 0.8414709848078965
my_sinus(1, 9) = 0.8414709848078965
Valeur de référence : math.sin(1) =  0.8414709848078965
$>

Le tutoriel Python complet (Text+Vidéos)

Le tutoriel Python en vidéos

Evaluez vos compétences en Python

Améliorations / Corrections