
Accès rapide :
La vidéo
Méthodes et classes abstraites
Faire usage de l'abstraction
Une classe abstraite ne peut pas être instanciée !
Implémentation de méthode abstraite
Utilisation de notre hiérarchie de classes
Travaux pratiques
Le sujet
La correction
Le concept d'interface
Syntaxe de définition et d'implémentation d'interfaces
Un cas concret
En Java, il y a des interfaces de partout
Assistance proposée par Eclipse pour implémenter vos méthodes abstraites
Utilisation de l'assistant de production de classes
Utilisation de la petite ampoule
Utilisation de la séquence de touches CTRL+SPACE
Travaux pratiques
Le sujet
La correction
Cette vidéo vous présente les concepts de méthodes abstraites et de classes abstraites, à l'aide d'un exemple de code adapté. Au terme de cette vidéo, la notion d'interface (quasiment équivalente à une classe totalement abstraite) est présentée.
Dans le chapitre précédent, nous avons commencé à nous familiariser avec le concept d'héritage. L'héritage permet donc de factoriser un certains nombre de méthodes pour un ensemble de types. Mais nous allons voir que parfois on aimerait factoriser un comportement mais sans que l'on soit en mesure de l'implémenter au niveau d'abstraction dans lequel on se trouve : dans ce cas nous définiront une (ou plusieures), méthode(s) abstraites(s).
Qu'est ce que cela veut dire ? Le mieux, pour comprendre la chose, est de considérer un exemple concret. Je vous propose de repartir de l'exemple de code que vous avez produit dans le TP précédent : à savoir, la gestion des classes de figures géométriques. Pour rappel, voici un diagramme UML montrant la hiérarchie de classe développée.
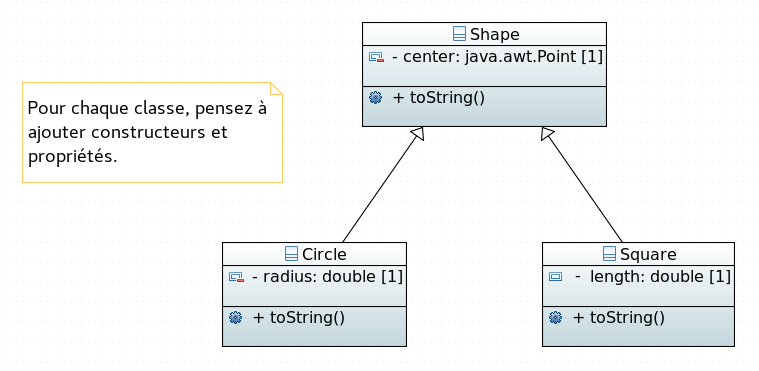
Si l'on considère cet exemple, il peut paraître naturel d'annoncer que l'on doit pouvoir calculer la surface de n'importe quelle figure géométrique.
Nous avons donc envie d'ajouter une méthode area, qui calcule une valeur flottante, au niveau de la classe Shape.
Mais comment implémenter une méthode de calcul de surface si on ne connait pas les spécificités de la figure géométrique ? C'est là qu'intervient le
concept de méthode abstraite : nous allons déclarer cette méthode, mais nous ne l'implémenterons pas ! Nous laisserons le soin aux sous-classes
de concrétiser la méthode.
Pour définir une méthode comme étant abstraite, il faut utiliser le mot clé abstract devant la méthode et, bien entendu, il ne faudra plus
mettre de corps de méthode (plus de paire d'accolades). Voici comment déclarer une méthode abstraite.
1 |
public abstract double area(); |
Cela va entrainer une autre modification : si une classe contient au moins une méthode abstraite, alors la classe doit, elle aussi, être définie ainsi.
Voici la nouvelle version de notre classe Shape intégrant cette méthode abstraite.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
package fr.koor.poo; import java.awt.Point; abstract public class Shape /* extends Object */ { // --- The center attribute --- private Point center; // --- 2 constructors --- public Shape() { this( new Point( 0, 0 ) ); } public Shape( Point center ) { // super(); // Appel au constructeur parent sous-entendu this.setCenter( center ); } // --- The center property --- public Point getCenter() { return center; } public void setCenter( Point center ) { if ( center == null ) { throw new NullPointerException( "center parameter cannot be null" ); } this.center = center; } // --- An abstract method for compute the area of the shape --- public abstract double area(); // --- A method for compute a shape representation string --- @Override public String toString() { return "Unknown shape placed at " + center; } } |
Il faut comprendre qu'arrivé à ce stade on ne peut plus directement utiliser notre classe Shape. Ce que j'entends par « directement »,
c'est que cette classe spécifie un comportement que l'on souhaite obtenir, mais sans l'implémenter. Cette classe est donc incomplète (abstraite).
Si vous pouvions créer une instance de cette classe, que se passerait-il si on invoquait la méthode area ? Et bien ça planterait le
programme ! Du coup, Java préfère retirer l'instanciation d'une classe abstraire plutôt que de générer des plantages à l'exécution.
Le test suivant vous montre de qui se passe si l'on cherche à produire une instance à partir de la classe Shape.
1 2 3 4 5 6 7 8 9 10 11 |
package fr.koor.poo; public class Start { public static void main( String [] args ) { Shape shape = new Shape(); } } |
Et voici le message d'erreur produit par le compilateur.
$> javac fr/koor/poo/Start.java
fr/koor/poo/Start.java:7: error: Shape is abstract; cannot be instantiated
Shape shape = new Shape();
^
1 error
$>
Mais alors, à quoi sert une classe abstraite qu'on ne peux pas instancier ? C'est simple, a imposer la présence de méthodes dans les classes filles.
Effectivement, pour l'heure, on ne peut pas non plus instancier un cercle ou un carré. Pourquoi ? Par-ce que ces deux classes héritent de la méthode
abstraite area. Donc pour l'heure Circle et Square sont aussi considérées comme abstraites ! Il faut donc,
obligatoirement redéfinir la méthode area dans nos classes de figures géométriques si l'on souhaite que le projet recompile.
Nous sommes d'accord, le calcul de surface d'un cercle et celui d'un carré sont bien deux traitements distincts. Donc chaque classe doit implémenter sa méthode de calcul de surface. Dans l'exemple de code suivant, je ne précise que la méthode manquante, je vous laisse reprendre le reste de la classe de la correction du chapitre précédent.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
package fr.koor.poo; import java.awt.Point; public class Circle extends Shape { // Begin of the class: attributes, constructors, properties, ... @Override public double area() { return Math.PI * this.radius * this.radius; } } |
Et on fait de même pour notre classe de manipulation de carrés.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
package fr.koor.poo; import java.awt.Point; public class Square extends Shape { // Begin of the class: attributes, constructors, properties, ... @Override public double area() { return this.length * this.length; } } |
area, vous êtes dans l'obligation de marquer cette classe comme
étant elle aussi abstraite : elle hérite d'une méthode abstraite, elle est donc abstraite.
Maintenant il nous faut revoire la classe de démarrage : on ne peut plus produire d'instance de Shape. Mais, si on y réfléchi, qu'est ce que cela voulais dire d'instancier une figure dont on ne connaissait pas exactement la nature ? C'est presque logique. Du coup, je n'y instancie plus que des cercles et des carrès.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
package fr.koor.poo; import java.awt.Point; import java.util.ArrayList; public class Start { public static void main( String [] args ) { ArrayList<Shape> shapes = new ArrayList<>(); shapes.add( new Circle( new Point( 5, 5 ), 1 ) ); shapes.add( new Square( new Point( 1, 1 ), -2 ) ); shapes.add( new Circle() ); for( Shape shape : shapes ) { System.out.println( shape + " -> " + shape.area() ); } } } |
Et voici les résultats produits par cet exemple de code.
$> java fr.koor.poo.Start A circle placed at java.awt.Point[x=5,y=5] and with a radius 1.0 -> 3.141592653589793 A square placed at java.awt.Point[x=1,y=1] and with a length 2.0 -> 4.0 A circle placed at java.awt.Point[x=0,y=0] and with a radius 1.0 -> 3.141592653589793 $>
Peut-être vous posez-vous une question arrivé à ce point : pourquoi être obligé de spécifier la méthode area au niveau de Shape
alors qu'on invoque que les redéfinitions de cette méthode au niveau de Circle et de Square ? Ne pourrions-nous pas enlever
la définition de la méthode abstraite sur Shape ? Et bien je vous propose de le tester et vous constaterez que le programme ne compilera plus.
Pourquoi ?
La réponse est simple, c'est pour que le polymorphisme puisse fonctionner. En fait, il y a deux étapes bien distinctes : la compilation puis
l'exécution du programme. Durant la phase de compilation, le compilateur ne peut pas savoir quelles seront les figures qui seront présentes dans la
collection. Donc la seule chose qu'il sait, c'est que la collection contiendra un ensemble de Shape. Effectivement, en ligne 10, la
collection est typée ArrayList<Shape> (c'est un type générique, nous reviendrons sur ce concept ultérieurement).
Notez qu'on retrouve bien ce type Shape quand on cherche à sortir un élément de la collection en ligne 16.
En conséquence, si l'on cherche à invoquer une méthode sur cet élément, cette méthode devra être définie sur le type de base : comme dans le for
on invoque la méthode area, nous devons donc la définir dans Shape (pour que ça compile) et comme à ce niveau de définition on ne sait pas
implémenter la méthode, on doit la définir abstraite.
La seconde étape, c'est l'exécution du programme. A ce stade, il faudra trouver la nature exacte de notre figure géométrique pour pouvoir invoquer la
bonne méthode. Et nous avons l'obligation d'avoir concrétisé la méthode sur les classes filles, sans quoi nous n'aurions pas pu faire les instaciations
(les new).
Ajouter une méthode abstraite de calcul de périmètre au niveau de la classe Shape et faîte en sorte de l'implémenter sur nos deux
classes filles. Voici un modèle UML présentant le contenu des classes souhaitées. Pour information, en UML, une méthode abstraite se note en
italique : ainsi, et avec un peu d'habitude, on repère facilement les méthodes abstraites proposées par un modèle (bon, il faut quand même les voir).
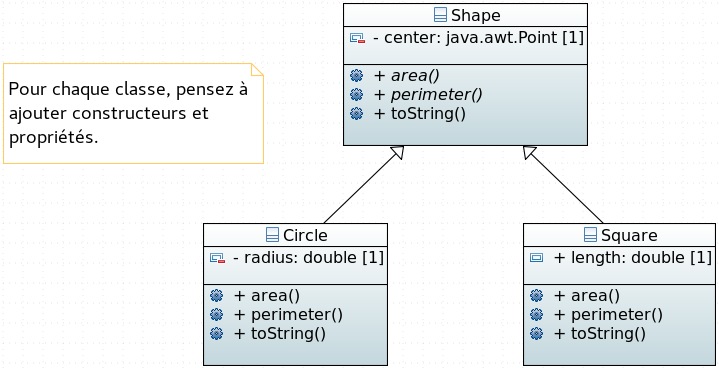
2*PI*rayon. Celle d'un carré est 4*longueur.
Les plus courageux d'entre vous pourront aussi ajouter une nouvelle classe Triangle, mais je ne proposerais pas de
correction sur ce point. Dans ce cas, mettez en attribut de cette classe un tableau de trois vecteurs reprensentant les positions des sommets du
triangle par rapport au centre de la figure. Vous devrez alors aussi fournir une nouvelle classe Vector constituée de deux attributs
(un décalage en X et un décalage en Y).
Etant donné que nous avions déjà corrigé certains de ces code dans le chapitre précédent (le chapitre relatif à l'héritage), je ne mettrais dans les code de corrections qui suivent, que les éléments importants relatifs à sujet du TP. Je vous laisse le soin de copier/coller les codes manquants à partir du chapitre précédent, si vous n'avez pas réussit à les produire. Nous commençons par définir notre nouvelle méthode abstraite.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
package fr.koor.poo; import java.awt.Point; abstract public class Shape /* extends Object */ { // BEGIN OF THE CLASS // --- An abstract method for compute the area of the shape --- public abstract double area(); public abstract double perimeter(); // END OF THE CLASS } |
Ensuite, il faut implémenter cette méthode abstraite dans nos différentes classes filles (Circle et Square).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
package fr.koor.poo; import java.awt.Point; public class Circle extends Shape { // Begin of the class: attributes, constructors, properties, ... @Override public double area() { return Math.PI * this.radius * this.radius; } @Override public double perimeter() { return 2 * Math.PI * this.radius; } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
package fr.koor.poo; import java.awt.Point; public class Square extends Shape { // Begin of the class: attributes, constructors, properties, ... @Override public double area() { return this.length * this.length; } @Override public double perimeter() { return 4 * length; } } |
Ensuite, testez vos méthodes de calcul de périmètre.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
package fr.koor.poo; import java.awt.Point; import java.util.ArrayList; public class Start { public static void main( String [] args ) { ArrayList<Shape> shapes = new ArrayList<>(); shapes.add( new Circle( new Point( 5, 5 ), 1 ) ); shapes.add( new Square( new Point( 1, 1 ), -2 ) ); shapes.add( new Circle() ); for( Shape shape : shapes ) { System.out.println( shape.perimeter() ); } } } |
Nous en avons pas tout à fait finit avec les types abstraits : il faut maintenant que nous parlions d'interface. Qu'est-ce qu'une interface ? En fait c'est presque la même chose qu'une classe abstraite, saut qu'une interface contient, très souvent, que des méthodes abstraites. Les interfaces sont très utiles du point de vue de la conception des librairies et vous en retrouverez un très grand nombre dans le Java SE ou dans le Java EE (Attention, on parle maintenant plutôt de Jakarta EE).
Syntaxiquement parlant, une interface s'introduit via le mot clé interface et il n'est pas nécessaire de mettre le mot clé
abstract : il est sous-entendu. Cette interface ne peut pas définir d'attribut d'instance.
Elle peut contenir des méthodes qui seront par défaut publiques et abstraites : il n'est donc pas nécessaire de spécifier les deux mots clés associés.
Voici un exemple de syntaxe.
1 2 3 4 5 6 7 8 9 10 11 |
public interface AnInterface { // Par défaut, une méthode d'interface est publique et abstraite. // Il n'est donc pas nécessaire de commencer par public abstract. void firstAbstractMethod( int param ); String secondAbstractMethod(); // Mais vous pouvez utiliser les deux mots clés si vous trouverez cela plus lisible public abstract void thirdMethod(); } |
Bien entendu, une interface étant un type abstrait, vous devez en dériver et implémenter ses méthodes abstraites. Du point de vue de la terminologie,
on préfère dire qu'on implémente l'interface plutôt qu'on en dérive (bien que cela ne soit pas faux). D'ailleurs, au lieu d'utiliser le mot clé
extends, on utilisera le mot clé implements pour produire cette classe dérivée. Voici un exemple d'implémentation d'interface.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
public class ConcreteClass implements AnInterface { @Override public void firstAbstractMethod( int param ) { // TODO: implémenter cette méthode } @Override public String secondAbstractMethod() { // TODO: implémenter cette méthode } @Override public void thirdMethod() { // TODO: implémenter cette méthode } } |
@Override afin d'indiquer que la première définition
de la méthode est située sur un type parent (dans notre cas, l'interface).
Petit, rappel, vous ne pouvez dériver que d'une seule classe mère. Par contre, vous pouvez dériver d'une classe et implémenter une autre interface. Dans ce cas l'implémentation d'interface sera obligatoirement placée après le lien d'héritage. De plus, vous pouvez implémenter autant d'interfaces que souhaité : il suffit de séparer leurs différents noms avec des virgules. Voici, encore une fois, un exemple de syntaxe.
1 2 3 4 5 |
public class ConcreteClass extends BaseClass implements FirstInterface, SecondInterfce { // TODO: implémenter toutes les méthodes requises. } |
Imaginons quelques instants que nous souhaitons développer un nouveau système d'exploitation. Et imaginons qu'actuellement nous soyons en train de travailler sur le support de l'impression. Comment pourrions-nous architecturer notre système ? Effectivement, nous devons prendre en charge une certaines difficultés : il existe un très grand nombre d'imprimantes et chacune d'entre elle supporte son propre protocole de communication. Comment pouvons-nous nous abstraire de cette multitude de protocoles de communication pour avoir un code de demande d'impression unique au niveau de notre système d'exploitation ? Bien que le sujet soit vaste, la réponse à ces questions n'est pas si complexe : il nous faut utiliser des interfaces !
L'idée, c'est de définir un driver (un pilote d'impression) générique : une, ou plusieurs, interfaces permettront de spécifier le comportement (les méthodes) de ce driver générique. Ensuite chaque fabriquant d'imprimante devra « hériter » de ce driver pour l'implémenter concrètement par rapport à leur matériel. Du point de vue du système d'exploitation, seul le driver sera vue et grâce au polymorphisme, nous déclencherons bien les méthodes adaptées, en fonction du matériel.
Je vous propose un petit diagramme UML pour synthétiser notre pensée. A savoir, en UML, on représente souvent une interface par un rond. Une autre possibilité consiste à garder un rectangle (symbolisant une classe) et à y rajouter dans le premier compartiment, un stéréotype interface. Un stéréotype UML, est une métadonnée et son nom est placé entre des doubles chevrons. C'est cette seconde représentation qui est utilisée dans le diagramme ci-dessous.
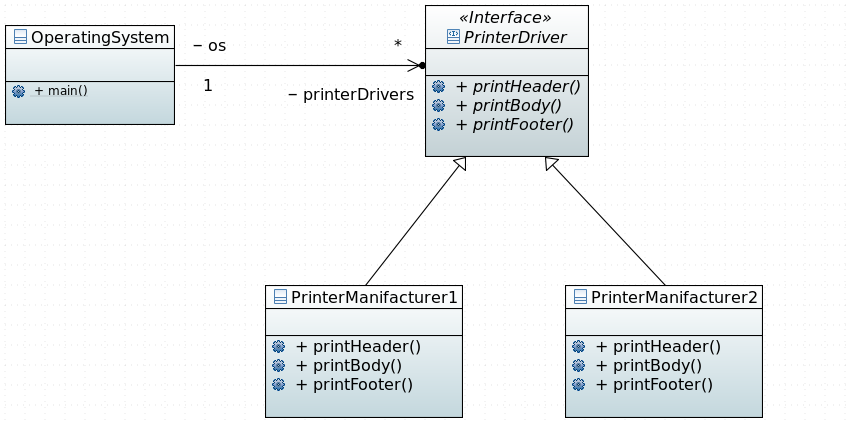
printHeader, printBody et printFooter. De même, normalement,
ces méthodes devraient accepter un certain nombre de paramètres : encore une fois, nous simplifions un peu les choses.
main de la classe OperatingSystem.
Il nous faut maintenant produire les codes correspondants à ce modèle UML. Je vais commencer par définir l'interface PrinterDriver.
Pour créer une nouvelle interface avec Eclipse, cliquez sur le projet ou sur un package du projet avec le bouton droit de la souris puis
sélectionnez les menus « New » puis « Interface ». Voici le menu contextuel proposé.
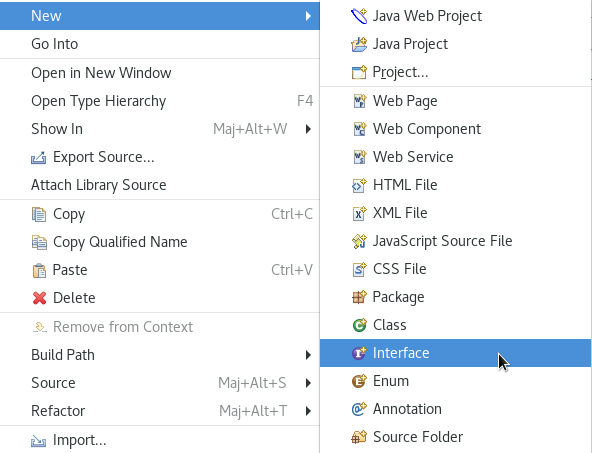
Une boîte de dialogue doit s'ouvrir afin de renseigner les informations nécessaires à la construction de cette interface. Vérifiez le package utilisé et donnez un nom à votre interface.
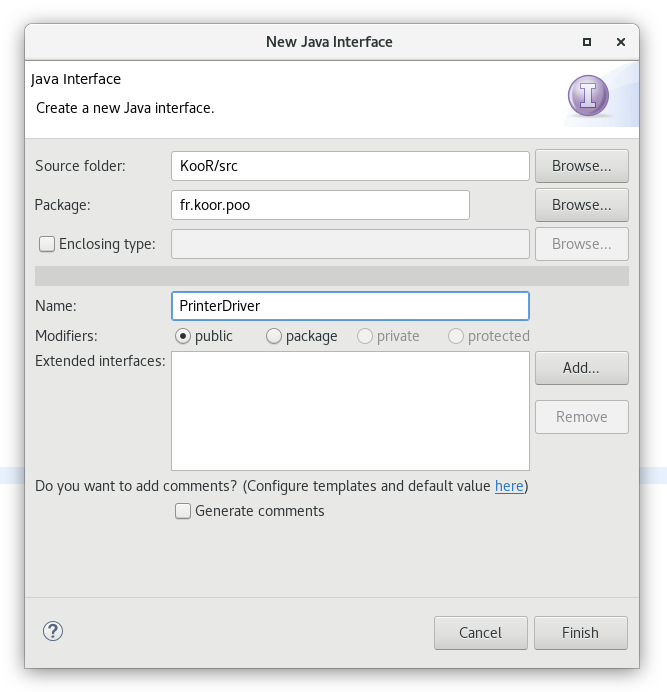
Voici le code de cette interface.
1 2 3 4 5 6 7 8 9 10 11 |
package fr.koor.poo; public interface PrinterDriver { void printHeader(); void printBody(); void printFooter(); } |
Ensuite, il nous faut des implémentations pour cette interface. On va imaginer avoir deux fabricants d'imprimantes qui ont choisi de proposer un driver pour notre système d'exploitation. Voici leurs implémentations.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
package fr.koor.poo; public class PrinterManifacturer1 implements PrinterDriver { @Override public void printHeader() { System.out.println( "Here i launch USB communication for print a header" ); } @Override public void printBody() { System.out.println( "Here i launch USB communication for print a body" ); } @Override public void printFooter() { System.out.println( "Here i launch USB communication for print a footer" ); } } |
Il est important de comprendre que notre interface est en quelque sorte un contrat ! Si dans l'implémentation d'un pilote d'impression une méthode est oubliée, alors la classe de pilote sera considérée comme abstraite et on ne pourra pas l'instancier. L'équipe de développement du système d'exploitation impose donc au fabriquant d'imprimante de respecter ce contrat. C'est trop fort ;-)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
package fr.koor.poo; public class PrinterManifacturer2 implements PrinterDriver { @Override public void printHeader() { System.out.println( "On lance une communication USB pour imprimer l'entête" ); } @Override public void printBody() { System.out.println( "On lance une communication USB pour imprimer le corp" ); } @Override public void printFooter() { System.out.println( "On lance une communication USB pour imprimer le pied de page" ); } } |
Maintenant nous allons chercher à utiliser nos drivers d'impression. Voici un exemple de code.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
package fr.koor.poo; import java.io.FileInputStream; import java.util.ArrayList; import java.util.List; import java.util.Scanner; public class OperatingSystem { private List<PrinterDriver> printerDrivers = new ArrayList<PrinterDriver>(); public OperatingSystem() { // Chargement d'un fichier de configurations des pilotes d'impressions enregistrés try ( Scanner scanner = new Scanner( new FileInputStream( "conf/PrinterDrivers.cfg" ) ) ) { while( scanner.hasNextLine() ) { String driverClassName = scanner.nextLine(); // On construit une instance à partir du nom de la classe de driver Class<?> metadata = Class.forName( driverClassName ); PrinterDriver driver = (PrinterDriver) metadata.newInstance(); printerDrivers.add( driver ); } } catch( Exception exception ) { exception.printStackTrace(); // No printer driver is injected to the system } } public List<PrinterDriver> getPrinterDrivers() { return printerDrivers; } // On part du principe que le premier driver est celui par défaut public PrinterDriver getDefaultPrinterDriver() { return printerDrivers.get( 0 ); } public static void main( String[] args ) { // --- On créer une instance de l'OS --- OperatingSystem os = new OperatingSystem(); // --- On récupère le pilote par défaut (le premier) --- PrinterDriver printerDriver = os.getDefaultPrinterDriver(); // --- On tente une impression --- printerDriver.printHeader(); printerDriver.printHeader(); printerDriver.printHeader(); } } |
Il est important de bien remarquer que dans cette dernière classe, il n'y a aucune référence aux classes concrètes d'implémentation de nos drivers.
Seul le fichier de configuration connaît les différentes implémentations. En voici son contenu : fichier conf/PrinterDrivers.cfg.
fr.koor.poo.PrinterManifacturer1 fr.koor.poo.PrinterManifacturer2
Si l'on change l'implémentation du pilote d'impression par défaut dans le fichier de configuration (c'est le premier), aucune autre modification de code n'est donc nécessaire.
Si l'on reprend l'exemple, ci-dessus, il y a plus d'interfaces utilisées que vous le pensez probablement. Effectivement, nous utilisons l'interface
PrinterDriver : ça c'est certainement clair pour vous. Mais de quelle nature est le type java.util.List utilisé pour
contenir nos pilotes d'impressions ? Et oui, c'est aussi une interface !
Pourquoi avoir introduit des interfaces au niveau de l'API des collections de Java ? Très bonne question. N'oubliez pas, en algorithmique il existe plusieurs structures de données permettant de contenir des données : les listes chaînées, les tableaux, les arbres (binaires ou non, équilibrés ou non), ... Chaque structure de données possède, de par son algorithmique, des avantages, mais aussi des inconvénients. Bien choisir la collection utilisée, en fonction des besoins de votre programme, peut avoir des impacts forts sur les performances de celui-ci.
Le type java.util.List représente donc un ensemble de données que l'on peut parcourir séquentiellement du premier élément au dernier.
C'est un type de base (une interface) qui est implémenté par différentes classes : java.util.ArrayList (un tableau dynamique non synchronisé
contre les accès concurrents), java.util.Vector (un tableau dynamique synchronisé contre les accès concurrents),
java.util.LinkedList (une liste doublement chaînée), ...
Si vous vous êtes trompé d'implémentation (donc que vous avez choisi la mauvaise classe) vous n'aurez qu'une seule modification à effectuer, la classe utilisée pour construire la collection, étant donné que le reste du programme n'utilise que les méthodes définies dans le contrat (l'interface). Voici donc une variante du code client de tout à l'heure qui utilise une liste chaînée (les modifications sont en lignes 4, pour l'import, et 10).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
package fr.koor.poo; import java.io.FileInputStream; import java.util.LinkedList; import java.util.List; import java.util.Scanner; public class OperatingSystem { private List<PrinterDriver> printerDrivers = new LinkedList<PrinterDriver>(); public OperatingSystem() { // Chargement d'un fichier de configurations des pilotes d'impressions enregistrés try ( Scanner scanner = new Scanner( new FileInputStream( "conf/PrinterDrivers.cfg" ) ) ) { while( scanner.hasNextLine() ) { String driverClassName = scanner.nextLine(); // On construit une instance à partir du nom de la classe de driver Class<?> metadata = Class.forName( driverClassName ); PrinterDriver driver = (PrinterDriver) metadata.newInstance(); printerDrivers.add( driver ); } } catch( Exception exception ) { exception.printStackTrace(); // No printer driver is injected to the system } } public List<PrinterDriver> getPrinterDrivers() { return printerDrivers; } // On part du principe que le premier driver est celui par défaut public PrinterDriver getDefaultPrinterDriver() { return printerDrivers.get( 0 ); } public static void main( String[] args ) { // --- On créer une instance de l'OS --- OperatingSystem os = new OperatingSystem(); // --- On récupère le pilote par défaut (le premier) --- PrinterDriver printerDriver = os.getDefaultPrinterDriver(); // --- On tente une impression --- printerDriver.printHeader(); printerDriver.printHeader(); printerDriver.printHeader(); } } |
Que ce soit en dérivant des classes abstraites ou en implémentant des interfaces, votre IDE peut vous assister dans l'implémentation de vos méthodes abstraites, ce qui est bien pratique. Dans le cas d'Eclipse, vous avez plusieurs moyens d'arriver à vos fins.
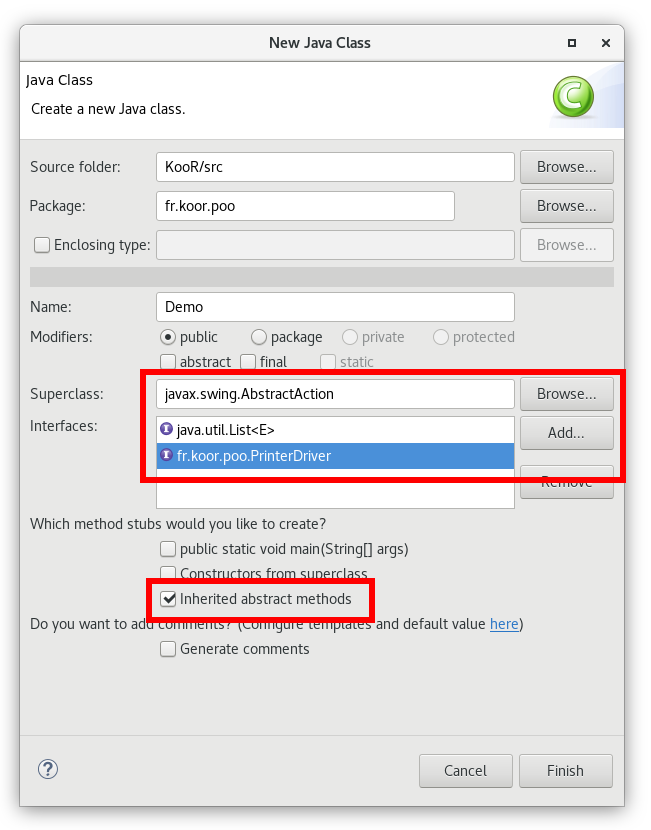
La première solution consiste donc à utiliser l'assistant de production de classes. Vous pouvez y spécifier une classe mère à hériter, mais aussi l'ensemble des interfaces à implémenter. Une fois ces éléments sélectionnés, il convient de vérifier que la case à cocher « Inherited abstract methods » soit bien cochées. Enfin cliquez sur « Finish » pour générer la nouvelle classe. Normalement, les squelettes des méthodes abstraites ont été automatiquement générés. Voici une capture d'écran de l'assistant.
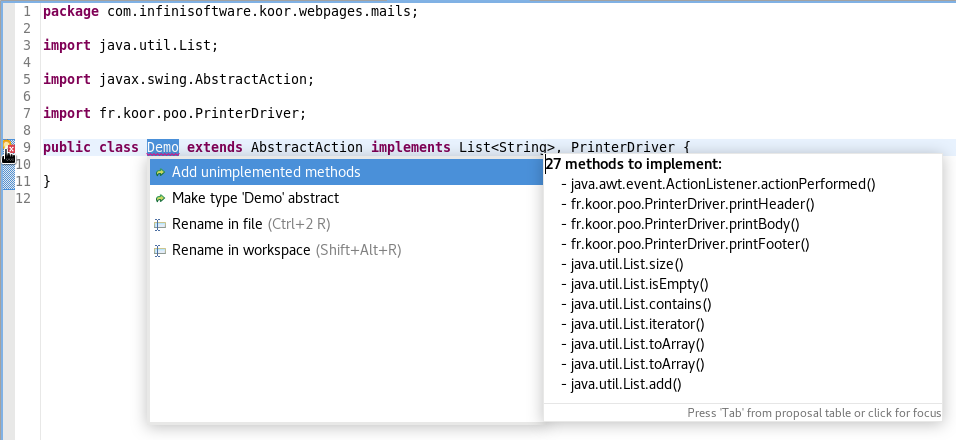
La seconde solution consiste à utiliser la petite ampoule qui s'affiche sur le côté gauche de l'éditeur. Si elle s'affiche c'est que vous avez produit la classe sans spécifier les types de bases dans l'assistant de création (classe et interfaces) et que vous venez de les rajouter dans l'éditeur. Comme, à ce moment-là, les méthodes abstraites ne sont pas surchargées, une erreur est produite et Eclipse vous propose de la corriger (l'ampoule pouvant s'interpréter comme « j'ai une idée »). Cliquez sur l'ampoule pour obtenir l'assistance à l'implémentation des méthodes abstraites.
Enfin, la troisième solution consiste à utiliser la séquence de touches CTRL+SPACE. Placez-vous à l'endroit souhaité pour générer une de vos
méthodes abstraites. Commencez à taper les premières lettres du nom de la méthode, puis enclenchez la séquence de touches. Normalement, la méthode
attendue doit être proposée dans le menu contextuel affiché. Sélectionnez là puis appuyez sur la touche ENTER/ENTREE.
Réitérer la manipulation pour chaque méthode manquante. Cette possibilité est surtout utile quand il vous manque qu'une unique méthode. Sinon, les deux
autres possibilités montrées précédemment me semblent plus efficaces.
L'interface java.lang.Runnable est proposée par le Java SE depuis sa première version. Elle spécifie la méthode run correspondant
à une tâche à exécuter. En voici sa définition :
1 2 3 4 5 6 7 |
package java.lang; public interface Runnable { /*public abstract*/ void run(); } |
Il est possible d'exécuter un Runnable dans un thread autonome (un fil d'exécution, permettant d'exécuter son traitement en parallèle du
thread principal exécutant la méthode main). Voici le code permettant de lancer un thread sur un Runnable;
1 2 3 |
Runnable runnable = new MyRunnableImplementation(); Thread thread = new Thread( runnable ); thread.start(); |
Notez aussi qu'il est possible de demander une pause en invoquant la méthode void Thread.sleep( long duration ) (la durée étant
exprimée en millisecondes). Un appel à cette méthode peut déclencher une exception : l'utilisation d'un bloc try / catch est
donc requis (nous reviendrons dans un futur chapitre sur la gestion des exceptions). Voici un exemple d'exécution.
1 2 3 4 5 |
try { Thread.sleep( 1000 ); // 1 seconde } catch( InterruptedException exception ) { exception.printStackTrace(); } |
Le but de la manipulation est simple. En vous basant sur les exemples de codes proposés ci-dessus, créer un thread gérant une file de
Runnable à exécuter eux-mêmes en parallèle. Tant qu'un Runnable est disponible dans la file, lancez son exécution dans un
thread autonome. Si aucun Runnable n'est disponible dans la file, le thread de la file d'attente fait une pause de 50 millisecondes
(pour ne pas saturer le CPU) puis revérifier si un nouveau message doit être lancé. La boucle pourra être infinie.
La file d'attente proposera une méthode void add( Runnable task ); pour permettre l'ajout d'une nouvelle tâche à exécuter. Les tâches
à exécuter pourront, par exemple, réaliser quelques d'affichage sur la console (chaque affichage étant espacés de quelques millisecondes, ainsi
vous pourrez constater l'alternance dans l'exécutions de vos tâches).
Votre méthode main doit démarrer la gestion de la file de messages et elle devra, de temps à autre, ajouter des nouvelles tâches à exécuter.
Bon courage. Comme d'habitude, ne passez pas à la correction immédiatement.
Pour réaliser ce TP, j'ai dû commencer par trouver une solution pour implémenter la file de Runnable. Il s'avère que dans le package
java.util nous avons une ... interface (et oui) Queue permettant d'obtenir un comportement de file. Ce type de collection
est générique (nous reviendrons sur la généricité plus tard) et peut donc contenir des Runnable.
Si vous ouvrez la Javadoc sur le type java.util.Queue vous pourrez y constater qu'il existe plusieurs implémentations pour cette interface.
Pour ma part, j'ai retenu le type java.util.ArrayBlockingQueue qui implémente une file sous forme d'un tableau à taille fixe.
Les accès y sont synchronisés, ce qui garanti qu'on peut utiliser ce type de données dans un environnement multithreadé (ce qui est notre cas).
Lors de l'instanciation d'un objet de ce type, je peux spécifier si je veux une gestion FIFO (First In/First Out) : second paramètre booléen.
Plutôt que de coder une boucle infinie sur la gestion de la file, je préfère avoir un attribut statique et publique, nommé isRunning,
permettant à mon code de savoir s'il doit poursuivre son exécution (valeur true) ou s'il doit s'arrêter (valeur false).
Voici le code de ma classe de gestion de ma file de tâches à exécuter.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
package fr.koor.poo; import java.util.Queue; import java.util.concurrent.ArrayBlockingQueue; public class RunnableQueue implements Runnable { private Queue<Runnable> runnables = new ArrayBlockingQueue<>( 100, true ); public static boolean isRunning = true; public void add( Runnable task ) { this.runnables.add( task ); } @Override public void run() { while( RunnableQueue.isRunning ) { // On lance un nouveau thread sur notre tâche (si elle existe). if ( this.runnables.size() > 0 ) { new Thread( this.runnables.poll() ).start(); } // On patiente un peu pour de nouveau voir si une // tâche doit être lancée. sleep( 50 ); } System.out.println( "RunnableQueue ended" ); } // On code cette méthode pour ne plus devoir utiliser le bloc try/catch public static void sleep( long duration ) { try { Thread.sleep( duration ); } catch ( InterruptedException exception ) { exception.printStackTrace(); } } } |
Ensuite, il nous faut coder des implémentations concrètes de tâches à exécuter. Je vous propose les deux classes suivantes : elles sont très proches, seul l'affichage change (faites preuve d'imagination en envisageant des traitements plus sérieux).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
package fr.koor.poo; public class FirstTaskType implements Runnable { private int index = 0; public FirstTaskType( int index ) { this.index = index; } @Override public void run() { for( int i=0; i<10; i++ ) { System.out.println( "FirstTaskType do something " + index ); RunnableQueue.sleep( 1000 ); } System.out.println( "FirstTaskType " + index + " terminated" ); } } |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
package fr.koor.poo; public class SecondTaskType implements Runnable { private int index = 0; public SecondTaskType( int index ) { this.index = index; } @Override public void run() { for( int i=0; i<10; i++ ) { System.out.println( "SecondTaskType do something " + index ); RunnableQueue.sleep( 1000 ); } System.out.println( "SecondTaskType " + index + " terminated" ); } } |
Et maintenant la classe de démarrage qui, elle aussi, implémente Runnable afin de créer ici et là des tâches à exécuter et les ajoute à la file de traitement.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
package fr.koor.poo; public class Start implements Runnable { private static RunnableQueue queue = new RunnableQueue(); @Override public void run() { int counter = 0; while( RunnableQueue.isRunning ) { int type = (int)( Math.random() * 2 ); int tempo = (int)( Math.random() * 10_000 ); Runnable task = ( type == 0 ? new FirstTaskType( counter ) : new SecondTaskType(counter) ); queue.add( task ); System.out.println( "New task started" ); counter++; RunnableQueue.sleep( tempo ); } } public static void main( String [] args ) { // On démarre une queue new Thread( queue ).start(); // On poste régulièrement des messages Start start = new Start(); new Thread( start ).start(); // On patiente un minute et on sort RunnableQueue.sleep( 120_000 ); // 2 minutes RunnableQueue.isRunning = false; } } |
Runnable afin de récupérer une instance produite à partir de l'une de nos
deux classes de tâches à exécuter.

Améliorations / Corrections
Vous avez des améliorations (ou des corrections) à proposer pour ce document : je vous remerçie par avance de m'en faire part, cela m'aide à améliorer le site.
Emplacement :
Description des améliorations :